Schilderen/Gulden snede

De gulden snede (in normale taal de "gouden verhouding") is een curiosum uit de compositieleer, die zelden wordt toegepast, hoewel velen een gulden snede proberen te zien in vooral oude en beroemde schilderijen.

Gulden sneden als percentages

De gulden snede is een manier om het vlak te verdelen. Het is een ingewikkeld verhaal, dat de mensheid al sinds de oudheid heeft gefascineerd. De Romeinen noemden deze verhouding "sectio divina", de goddelijke verdeling.

Wiskundige truc

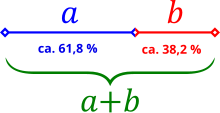
De gulden snede is een wiskundige truc. Je kan een lijnstuk verdelen in twee delen volgens de gulden snede. Het ene deel heeft een lengte a, het andere deel lengte b. De lengte van het gehele lijnstuk is dan a+b,Dan geldt voor de gulden snede:

De lengteverhouding tussen b en a is gelijk aan de verhouding tussen a en de totale lengte (a+b).

Deze verhouding wordt aangegeven met het symbool φ en heeft een waarde van 1.618... (${\frac {1+{\sqrt {5}}}{2}}$). Eenvoudiger kan je stellen dat lijnstuk a ca. 61,8% is van de totale lengte, lijnstuk b 38,2%, zoals aangegeven in de figuur.

	Van een schilderij als de Mona Lisa zijn allerlei analyses gemaakt in relatie tot de gulden snede. Kies maar wat je ervan aanstaat om in je eigen werk toe te passen.

Gouden rechthoeken

Toepassing van de gulden snede

Gouden rechthoeken

De gulden snede heeft fascinerende eigenschappen. Als je van het geschetste blauwe lijnstuk hierboven een vierkant maakt, dan ontstaat een gouden rechthoek. De zijden van die rechthoek hebben dan de verhouding van de gulden snede. Ook voor de kleinere rode rechthoek geldt dat de zijden de verhouding van de gulden snede hebben.

Zo kan je doorgaan, en er nog een groen vierkant aan vastzetten.

Een gulden rechthoek kan je oneindig in vierkanten onderverdelen

Omgekeerd kan je, als je een doek hebt met zijden volgens de gulden snede, er een vierkant in tekenen. Dan houd je een een kleinere rechthoek over, die weer de verhouding van de gulden snede heeft. Daar kan je dan ook een vierkant intekenen, etc. Zo kan je een rechthoek volgens de gulden snede in oneindig veel vierkanten opdelen. Als je de hoeken van de vierkanten met elkaar verbindt, krijg je een spiraal, zoals aangegeven in één van de Mona Lisa's.

Pentagram

Bijzonder is ook dat de afmetingen van een vijfpuntige ster, het pentagram, ook verhoudingen hebben volgens de gulden snede.

Doek met de verhouding van de gulden rechthoek

Om dit allemaal toe te passen in je werk, zou je kunnen uitgaan van een doek met afmetingen volgens de gulden rechthoek, dat wil zeggen dat de lengte 1,618 keer zo groot is als de breedte, bijvoorbeeld van een doek van 64,7 x 40 cm. Zo een doek is standaard niet in de handel (Zie het hoofdstuk Afmetingen en vormen). Zo een doek of paneel zou je dus zelf op maat moeten maken.

N.B. Papier met de A-formaten heeft verhoudingen van de zijden van 1:1,414 (${\sqrt {2}}$)

Sandro Botticelli - De geboorte van Venus, geschilderd tussen 1483 en 1485, heeft precies de afmetingen van de gulden rechthoek

Alma Tadema - Ook dit schilderij, met als titel de Rozen van Heliogabalus, heeft afmetingen van de gulden rechthoek

Toepassing op een willekeurig doek

Je kan de gulden snede ook toepassen op een doek met willekeurige afmetingen. Je verdeelt het doek dan in de delen 62,8% en 31,2% en gebruikt de resulterende punten en lijnen als basis voor je schilderij. Of je zet een gulden rechthoek ergens in je schilderij, en verdeelt dat in vierkanten en andere gulden rechthoeken.

Esthetisch ideaal?

Over de vraag of de gulden snede gezien moet worden als een esthetisch ideaal of als een wiskundig interessant verschijnsel zijn de deskundigen het niet eens. In elk geval denkt men dat de gulden snede in de architectuur uit de klassieke oudheid werd toegepast.

Het verschil met de regel van derden

Het verschil tussen de derden-regel (rode lijnen) en de gulden snede (blauwe lijnen)

De gulden snede lijkt wel enigszins op de derden-regel die in de compositie ook wel wordt toegepast. De lijnen bij de derden-regel liggen op 33% vanaf de rand van het schilderij. Bij de gulden snede liggen die lijnen op 38,2%.